מבוא
על מה הספר? למי הוא מיועד?
הספר הזה (או "מיני-ספר", כפי שאני מעדיף להתייחס אליו) מלמד על מבני נתונים, תוך מתן דוגמאות מעולם המשחקים. לגמרי במקרה, הספר משתמש בשפת פייתון לשם כתיבת קוד של ממש - וזאת משתי סיבות:
- שפת פייתון היא שפה נקייה ופשוטה יחסית, ועם זאת תומכת בשיטות פיתוח מודרניות (נכון להיום), כגון תיכנות מונחה-עצמים, תיכנות פונקציונאלי ושאר מילים גבוהות שאהובות על פרופסורים למדעי המחשב.
- הספר הזה נועד לשמש חומר ללימוד-עצמי לתלמידי קורס "פייתון לבית-ספר, או בית-ספר לפייתון". בנסיבות אלו, השימוש בשפת פייתון הוא מחוייב המציאות...
הספר מיועד למי שמעוניין ללמוד על תיכנות ברמה מעמיקה יותר מאשר "לקודד תוכניות", על-מנת להגיע ליכולת לכתוב משחקים כגון דמקה, "מבוכים ודרקונים", או להכיר נושאים לא-קשורים לכאורה כגון דחיסת תמונות או שיטות מיון.
שימו לב - הספר מניח שהקוראים (אתם!) יודעים לתכנת בשפת פייתון, ומכירים שיטות תיכנות בסיסיות כגון כתיבת פונקציות, הגדרת מחלקות ועצמים וכיוצא בזה. אם למשל הגעתם לחודש השלישי בקורס "פייתון לבית-ספר, או..." - זהו זמן טוב להתחיל.
איך כדאי לקרוא את הספר?
ראשית - איך לא כדאי לקרוא את הספר הזה. לא כדאי לקרוא את הספר הזה מהתחלה ועד הסוף - לשם כך קיימים ספרי קריאה, ועם כל הכבוד למבני נתונים, קשה להתחרות בשר הטבעות, נשים קטנות והנסיך הקטן. להמלצה זו יש שני טעמים. האחד - הספר מכיל סיפורים על נושאים שונים, שעשויים לדבר לאנשים שונים, ולכן אפשר לקרוא רק חלקים מתוכו. השני - לימוד תיכנות מתבצע בעיקר דרך אצבעות הידיים (אפשר לנסות להקליד באמצעות איברים אחרים אם ממש חייבים) - קריאה בלבד אינה מלמדת את הדברים החשובים, ולכן מומלץ לקחת את הקוד לידיים, לנסות על המחשב, לשנות מעט ואפילו (*אוי, ההלם, ההלם!*) לכתוב דברים משלכם.
וכעת, איך באמת לקרוא את הספר הזה? התשובה היא - ביחרו לעצמכם את היעד, וקיראו את מה שצריך על-מנת להגיע אליו. כל אחד מהפרקים ה' ומעלה מהווה נושא ומוביל לאוסף משחקים בעל אופי מסויים. ביחרו את פרק היעד שהייתם מעוניינים להגיע אליו, ובראשיתו תמצאו מפה. המפה מכילה את רשימת הפרקים המוקדמים שמומלץ לקרוא, על-מנת ללמוד מה שדרוש כדי להבין את הפרק המסויים. המפה מכילה לא רק רשימת פרקים - אלא גם עד כמה צריך להעמיק בכל אחד. למשל, על מנת ללמוד על גרפים (עבור משחקי "מבוכים ודרקונים"), יש ללמוד על מבני יסוד במבני נתונים - אבל נושא הסיבוכיות לא מאוד חשוב.
לבסוף, תוך-כדי קריאה של כל אחד מהפרקים, ניתנות דוגמאות - הקלידו אותן במחשבכם והפעילו אותן. הוסיפו הדפסות ביניים כדי שתראו בדיוק מה מתרחש. שנו אותן וראו כיצד השינוי משפיע. נסו להוסיף לדוגמאות תכונה חדשה - אולי שיפור יעילות, אולי הוספת יכולת חדשה... כתיבת קוד היא הדרך היחידה בה תלמדו לתכנת באמת...
מה עם "התשובות הנכונות"?
בהרבה ספרי לימוד ישנו נספח עם התשובות הנכונות לתרגילים. מנהג מגונה זה מוביל, לטעמי, לשתי תופעות - אצל העצלנים הוא משמש כפיתוי לא לנסות לכתוב לבד. הרבה יותר קל לכתוב קוד אחרי שראית אותו כבר. אצל החרוצים - הם ממילא יכתבו את הקוד, ויבדקו אותו, וינסו נסיונות חדשים, וישפרו אותו. כך או כך - הפתרונות לא ממש נחוצים.
בנוסף, בכתיבת תוכנה אין "תשובה נכונה" - את אותה התוכנית ניתן לכתוב בדרכים שונות בעלות יתרונות וחסרונות שונים. השאלה "איך יותר נכון לכתוב תוכנית שעושה כך וכך" אינה שלמה - התשובה תלויה בנסיבות שונות, כגון מתי התוכנית צריכה להיות מוכנה, עד כמה הדרישות צפויות להשתנות עבור גרסאות עתידיות, מה מטרת כתיבת התוכנית וכו'. אפילו בספר לימוד כמו זה - אתם קובעים את מטרת התוכניות - ולכן אתם תצטרכו לבחור את הדרך הנכונה לכתוב אותן.
זהו, קחו כוס מים, עט ונייר ומחשב, והכינו לכם מפת קריאה...
קצת על מבני נתונים
כשכותבים תוכנה, יש לנו בדרך כלל שני חלקים - קוד ונתונים. לכתוב קוד זה קל - לנהל נתונים הוא החלק המסובך, בדרך כלל. בואו נקפוץ לבריכה המכונה "מבני נתונים", כדי להפוך חלק זה של התכנות לפחות מסובך.
מהו מבנה נתונים?
מבנה נתונים הוא רכיב תוכנה המאפשר לנו לשמור נתונים, ולבצע עליהם פעולות מסוגים שונים, כגון הוספת נתון, מחיקת נתון, חיפוש נתון. מבנה נתונים נראה בעיקרון כך:
.----------------.
| 1 9 |
| 8 10 |
| |
| 123 |
| |
'----------------'
טוב, מבני נתונים לא באמת נראים כך. כל מבנה נתונים "נראה" קצת אחרת, כפי שנראה
בהמשך.
למה צריך מבני נתונים?
עד כמה שהדבר ישמע מוזר, כל תפקידה של תוכנה הוא לארגן נתונים. לקלוט נתונים, לעבד אותם ולפלוט אותם בחזרה. קחו למשל משחק כמו שחמט - התוכנה קולטת את הוראות השחקן, מעבדת אותן לכדי ביצוע מהלך, ומציגה על המסך את הלוח במצבו החדש.
כדי שהתוכנה תוכל לבצע זאת, היא עשויה להצטרך לחשב הרבה חישובים, וכל החישובים הללו עוסקים בנתונים - מיקומם של הכלים השונים, המהלכים המותרים לכל כלי, "שווים" של הכלים השונים ומידת היתרון שמקנה מיקום כל כלי.
מאחר ומספר המהלכים השונים האפשריים הוא עצום, רצוי שהנתונים יישמרו באופן שניתן יהיה לחשב חישובים בצורה יעילה - איננו רוצים משחק שחמט ממושב שזקוק לשעה לביצוע כל מהלך!
אילו תכונות מעניינות אותנו לגבי מבנה נתונים כלשהו?
במחשב כמו שאנחנו מכירים אותו יש שני משאבים מוגבלים - כוח חישוב (נגזר ממהירות המעבד, אבל לא רק) וכמות זיכרון. על מנת שנוכל לכתוב תוכנה יעילה, מבני הנתונים שאנחנו משתמשים בהם צריכים לאפשר לנו לעבוד כך ש:
- הפעולות שאנחנו מעוניינים לבצע עליהם תהיינה מהירות ככל האפשר (תצרוכנה כוח חישוב מינימלי).
- כמות הזיכרון הדרושה לשם שמירת הנתונים ומבנה הנתונים תהיה קטנה ככל האפשר.
הבעיה, כפי שנראה בהמשך, היא שאלו שתי דרישות מנוגדות. מבנה נתונים שדורש מעט זיכרון לרוב זקוק להרבה כוח חישוב לשם ביצוע פעולות עליו. מבנה נתונים המאפשר לבצע פעולות באמצעות כוח חישוב מינימלי - עושה זאת על-ידי שימוש ביותר זיכרון.
מכאן ואילך, נראה מבני נתונים מסוגים שונים, המאזנים את דרישות כוח החישוב והזיכרון בדרכים שונות. יש המון סוגי מבני נתונים, משום שלכל תוכנה יש צרכים שונים מעט. זה נשמע מאוד "באוויר" כרגע, אולם כשנראה מה מאפשרים מבני נתונים שונים, העניין יהיה ברור יותר. ובכן - הבה נתחיל במסע.
מושגי יסוד במבני נתונים
לפני שנפגוש מבני נתונים מסויימים, כדאי שנכיר כמה מושגי יסוד - מעין מילון של מושגים, שיאפשרו לנו לדבר באופן ברור יותר - במקום להגיד "אוסף של נתונים שמסודרים בטור ואפשר לפנות לכל אחד לפי מיקומו בטור", נוכל פשוט לאמר "מערך" - וכולנו נבין במה מדובר.
גרפים - צמתים, קשתות ומה שביניהם
בתאוריה של מדעי המחשב, מקובל להשתמש במושג "גרף" די לתאר כל דבר מעניין. עד-כדי כך המושג הזה שימושי, שפותחה תאוריה מתמטית שלימה המכונה בשם "תורת הגרפים", וכל הפרופסורים למחשבים, כשרוצים לפתור בעיה, יגידו משהו כגון "המממ... אפשר לתאר את הבעיה הזו כמו גרף הנראה כך וכך, ואז יש שיטה מוכרת מתורת הגרפים הנקראת כך-וכך, והיא מאפשרת לפתור את הבעיה". כפי שאתם רואים, בשביל פרופסור למחשבים, לכל הילדים קוראים "דני" - וכשקוראים להם "דני" - יותר קל להסתדר איתם...
ובכן, גרף הוא מבנה המורכב מצמתים, וקשתות. את הצמתים מציירים לרוב כמו עיגולים,
והקשתות הן קווים המחברים בין העיגולים... סליחה, הצמתים. משהו כמו זה:
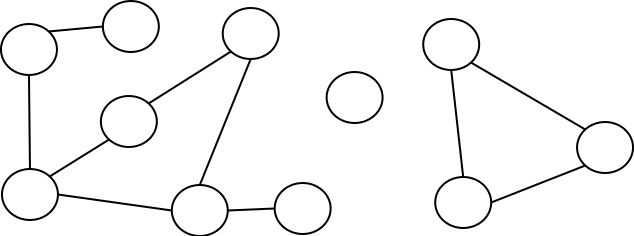
שימו לב לכמה דברים לגבי הגרף שלנו:
- עשויות להיות צמתים שאינן מחוברות לאף צומת אחרת.
- ייתכן שהגרף מחולק בפועל לתת-גרפים, שאין ביניהם שום קשת.
- גרף שכל הצמתים בו מחוברות באופן כלשהו (כלומר, מכל צומת אפשר להגיע לכל צומת אחרת במסלול כלשהו), נקרא בשם "גרף קשיר".
בנוסף, גרפים מחולקים לשני תת-סוגים - מכוונים ובלתי מכוונים. גרף מכוון הוא גרף
בו לכל קשת יש כיוון - מצומת אחת לצומת השניה. הגרף הקודם שראינו הינו גרף
בלתי-מכוון. הנה דוגמא לגרף מכוון:
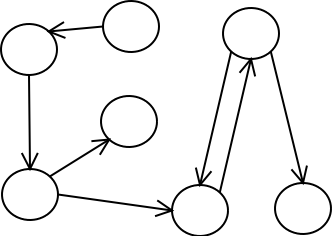
שימו לב לכמה תכונות של גרף מכוון:
- גרף מכוון יכול להכיל קשתות שנראות מספיקות, ועדיין יהיה בלתי אפשרי להגיע מצומת מסויימת לצומת אחרת (בגרף שלנו, למשל, מהצומת הימנית התחתונה אי אפשר להגיע לצומת הימנית העליונה).
- יש משמעות לשתי קשתות בין אותן שתי צמתים - כדי לאפשר להגיע מצומת אחת לשניה ובחזרה.
לבסוף, ניתן לשמור מידע בצמתים ו/או בקשתות של הגרף - בדרך כלל מספרים, אבל לפעמים
מידע מסוג אחר. הנה גרף עם מספרים בצמתים:
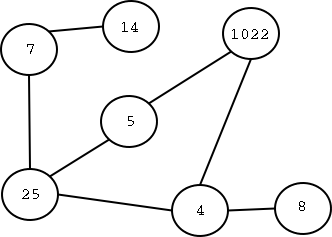
כפי שנראה בהמשך, יש הרבה מאוד שימושים לגרפים. אפשר לייצג באמצעותם, למשל, מפת כבישים. כל צומת תהיה עיר, וקשת בין ערים מייצגת כביש בין שתי הערים. ניתן להצמיד מספר לכל קשת כזו המתאר את המרחק, בקילומטרים, בין שתי הערים. אם הגרף מכוון, הוא מאפשר לנו למשל להראות כבישים חד-סטריים ודו-סטריים (שתי קשתות הפוכות בין אותן שתי צמתים יכולות לייצג כביש דו-סיטרי). קצת דמיון, והגרף מתאר מבוך מתחת לאדמה, המורכב מחדרים ומתעלות המקשרות ביניהם. גרף מכוון יכול לתאר את כלי הדם בתוך הגוף שלנו. בקצרה - גרף יכול לתאר (כמעט) כל דבר...
פעולות בדידות על מבני נתונים - הוספת נתון, מחיקת מתון, חיפוש נתון
את הפעולות הניתנות לביצוע על מבנה נתונים ניתן לחלק לפעולות בדידות ופעולות כוללניות. הפעולות הבדידות הן פעולות המטפלות בנתון אחד. פעולות אלו עשויות להיות:
- הוספת נתון חדש לתוך מבנה הנתונים.
- מחיקת נתון קיים ממבנה הנתונים.
- חיפוש נתון במבנה הנתונים, לפי קריטריון כלשהו.
- שינוי תכונה כלשהי של נתון קיים במבנה הנתונים (למשל, במבנה נתונים המתאר מכוניות, ניתן יהיה להשתמש בפעולה המשנה את צבעה של מכונית).
פעולות כוללניות על מבני נתונים - מיון, חיפוש תת-קבוצה...
פעולות כוללניות על מבנה נתונים עשויות להשפיע על מספר נתונים בבת אחת. הנה כמה דוגמאות:
- מיון - פעולה זו מסדרת את הנתונים לפי סדר כלשהו (רשימת מספרים - מהקטן לגדול, רשימת צבעים - מהבהיר לכהה, וכדומה).
- חיפוש תת-קבוצה - מוצאת במבנה הנתונים קבוצה של נתונים המתאימים לקריטריון מסוים (למשל, ברשימת מספרים - מציאת כל המספרים הגדולים משבע).
מדידת יעילות של מבני נתונים - סיבוכיות מקום וסיבוכיות זמן.
מאחר וציינו שמבני נתונים אמורים לחסוך לנו זמן חישוב וצריכת זיכרון, פיתחו בשבילנו הפרופסורים למדעי המחשב שיטה להשוואת היעילות של מבני נתונים שונים - ובתור פרופסורים הם קראו לשיטה הפשוטה הזו בשם "סיבוכיות". ליתר דיוק, "סיבוכיות זמן" ו-"סיבוכיות מקום".
סיבוכיות זמן מתארת כמה זמן תימשך פעולה על מבנה הנתונים, ביחס לכמות הנתונים באותו מבנה, במקרה הגרוע ביותר. בדרך כלל, ככל שיש יותר נתונים במבנה, פעולות עליו תימשכנה זמן רב יותר - השאלה היא באיזה יחס.
ניקח למשל רשימה של נתונים המסודרת בזכרון. כדי לחפש נתון כלשהו ברשימה, יש צורך לסרוק את הרשימה מצד אחד לצד השני, עד למציאת הנתון. במקרה הכי גרוע, הנתון נמצא בקצה השני של המערך, ולכן סיבוכיות פעולת החיפוש ברשימה של N נתונים, היא N, או כפי שנהוג לסמן - "O)N)".פעולת הכנסת נתון חדש לרשימה ניתנת לביצוע באופן מיידי - למשל אם ננהג בשיטה הישראלית, ונוסיף את הנתון החדש התחילת הרשימה (הוא "נדחף" לפני כל האחרים). פעולה זו לוקחת תמיד אותו משך זמן, ללא תלות בכמות הנתונים ברשימה, ולכן נסמן את הסיבוכיות שלה כ-"O)1)".
סיבוכיות מקום, לעומת זאת, מתארת כמה זיכרון דורש מבנה הנתונים, ביחס לכמות הנתונים. ברשימה, למשל, יש צורך באיבר אחד עבור כל נתון, ולכן עבור N נתונים יש צורך ב-"O)N)" מקום בזיכרון. בהמשך נראה מבני נתונים שבהם צריכת הזיכרון גדולה יותר, כדי להשיג מהירות רבה יותר בביצוע פעולות.
אחרי שסיבכנו את עצמנו עם כל הסיבוכיות הזו, אפשר להתחיל עם מה שרצינו למעשה - להכיר מבני נתונים שונים, מבחוץ ומבפנים.
שיעורון א' - רשימות ומערכים
לפעמים מתייחסים אליהם כמובנים מאליהם, מתעלמים מהגאוניות הבסיסית שבהם - רשימות, ומערכים. חישבו על קפיצת הדרך שעשה האדם הקדמון כאשר למד סוף-סוף לספור: אחד, שניים, הרבה. ה-"הרבה" הזה הוא הרשימה, ובגילגולה המתוחכם יותר - המערך.
מהי רשימה? למה היא טובה?
רשימה היא אוסף של איברים המצביעים מהאחד לשני. לרוב יש לנו הצבעה לתחילת הרשימה,
וכדי לנוע על הרשימה אנו מתחילים מהמצביע הראשוני הזה, וסורקים לאורך הרשימה. ניתן
לתאר רשימה באמצעות גרף מכוון:

רשימה כזו נקראת גם "רשימה חד-כיוונית", משום שאפשר לסרוק אותה בכיוון אחד בלבד.
ישנן גם רשימות דו-כיווניות, הנראות כך:

רשימה מאפשרת לנו לשמור נתונים בצורה המאפשרת הוספה מהירה יחסית, אם כי זמן מציאת נתון ברשימה עשוי להיות ממושך. כשכמות הנתונים לא גדולה במיוחד, או כשכמעט אין צורך לבצע חיפושים ברשימה, רשימה מקושרת היא מבנה נתונים אידיאלי. למשל, כדי לשמור תור, אין צורך לבצע חיפושים - נתונים חדשים נכניס בסוף התור, ונתונים ישנים נוציא מתחילת התור.
מהו מערך?
מערך הוא מבנה נתונים המאפשר לגשת לכל נתון ביעילות לפי מיקומו. קשה לייצג מערך
באמצעות גרף, כך שנשתמש בשירטוט אחר:
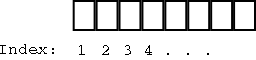
המערך מאפשר לגשת לתא כלשהו לפי אינדקס בצורה יעילה מאוד, אולם הוספת נתונים למערך (במיוחד באמצעו) היא פעולה פחות יעילה.
השוואת רשימה ומערך מבחינת יעילות
הבה ונשווה בין רשימה חד-כיוונית, רשימה דו-כיוונית ומערך, מבחינת סיבוכיות הזמן של ביצוע פעולות עליהם:
| /מבנה הנתונים הפעולה/ |
רשימה חד-כיוונית | רשימה דו-כיוונית | מערך |
|---|---|---|---|
| יצירת מבנה-נתונים חדש | (1)O | (1)O | (1)O |
| הוספת איבר בתחילת המבנה | (1)O | (1)O | (O(N - ייתכן שצריך להקצות מערך גדול יותר ולהעתיק לתוכו את כל הנתונים הישנים |
| הוספת איבר בסוף המבנה | (O(N - צריך לסרוק עד הקצה ואז להוסיף | (1)O | (O(N - ייתכן שצריך להקצות מערך גדול יותר ולהעתיק לתוכו את כל הנתונים הישנים |
| שליפת האיבר במקום ה-m במבנה | (O(N - צריך לסרוק עד המקום ה-m | (O(N - צריך לסרוק עד המקום ה-m | (1)O - הפעולה המקובלת עם מערכים |
| חיפוש איבר לפי קריטריון כלשהו | (O(N - צריך לסרוק עד שמוצאים | (O(N - צריך לסרוק עד שמוצאים | (O(N - צריך לסרוק עד שמוצאים |
ניתן לראות שמערך יעיל במיוחד אם יודעים מראש כמה איברים יהיו בו, וכך ניתן להקצות אותו מראש בגודל הנכון. רשימות מתאימות יותר כאשר איננו יודעים מראש את מספר האיברים, ויתכן שנרצה להוסיף ולהוריד איברים במהלך ריצת התוכנית.
רשימות ומערכים בפייתון
רשימות בפייתון הן עניין של מה-בכך. השפה תומכת ברשימות באופן בסיסי, ואנחנו איננו צריכים להתעסק ביצירות הקישורים מאיבר לאיבר, או בניהול הזיכרון כאשר מוסיפים איברים או מורידים איברים מהרשימה. אולם, רשימות בפייתון ממומשות, למעשה, כשילוב של מערך עם רשימה. ישנו מבנה נתונים הנקרא "תור דו-כיווני" (deque) - הבנוי בפועל כרשימה דו-כיוונית - נוסיף אותו למדידותינו, כפי שנציג מייד.
מערכים בפייתון גם הם דבר של מה-בכך - כבר השתמשנו בהם מזמן. לא דיברנו על יעילותם, עד כה. מאחר ופייתון היא שפה שנועדה להקל על המשתמשים, היא מסתירה מאיתנו את הפרטים הטכניים המרגיזים - למשל, הצורך להקצות זיכרון חדש כאשר מגדילים את גודלו של מערך, ולהעתיק את התוכן הישן לחדש. כיוון שכך, מבחינת כתיבת תוכניות - יותר קל להשתמש במערכים מאשר ברשימות. אולם, אם נשווה את הביצועים של שימוש בתורים דו-כיווניים לעומת שימוש במערכים, נראה הבדל גדול.
לשם המחשה, בואו נשווה את זמן הריצה של שלוש התוכניות הבאות. שלושתן מבצעות את אותה הפעולה - יצירת רשימה סדורה של מספרים, הכנסתם למבנה הנתונים, ולבסוף מחיקת כל המספרים ממבנה הנתונים לפי הסדר. התוכנית הראשונה משתמשת ברשימה, התוכנית השניה משתמשת במערך, והשלישית משתמשת בתור דו-כיווני. בואו נשווה את זמן הריצה של שלוש התוכניות עבור כמויות איברים שונות.
תוכנית א' - עם רשימה (list).
#!/usr/bin/env python2.4
import sys
if (not len(sys.argv) == 2):
print "Usage: ", sys.argv[0], "<number of elements>"
sys.exit(1)
elem_count = int(sys.argv[1])
print "elem_count - ", elem_count
# create a list with the given number of elements.
elem_id = 0
list = []
while elem_id < elem_count:
list.append(elem_id)
elem_id = elem_id + 1
# delete all the elements in the list from first to last.
elem_id = 0
while elem_id < elem_count:
list.pop(0)
elem_id = elem_id + 1
print "done"
תוכנית ב' - עם מערך (array).
#!/usr/bin/env python2.4
import sys
import array
if (not len(sys.argv) == 2):
print "Usage: ", sys.argv[0], "<number of elements>"
sys.exit(1)
elem_count = int(sys.argv[1])
print "elem_count - ", elem_count
# create an array with the given number of elements.
elem_id = 0
arr = array.array('i')
while elem_id < elem_count:
arr.append(elem_id)
elem_id = elem_id + 1
# delete all the elements in the array from first to last.
elem_id = 0
while elem_id < elem_count:
arr.pop(0)
elem_id = elem_id + 1
print "done"
תוכנית ג' - עם תור דו-כיווני (deque) - נתמך מגירסא 2.4 של פייתון.
#!/usr/bin/env python2.4
import sys
from collections import deque
if (not len(sys.argv) == 2):
print "Usage: ", sys.argv[0], "<number of elements>"
sys.exit(1)
elem_count = int(sys.argv[1])
print "elem_count - ", elem_count
# create a deque with the given number of elements.
elem_id = 0
dq = deque([])
while elem_id < elem_count:
dq.append(elem_id)
elem_id = elem_id + 1
# delete all the elements in the deque from first to last.
elem_id = 0
while elem_id < elem_count:
dq.popleft()
elem_id = elem_id + 1
print "done"
הבה נשווה את זמן הביצוע של כל אחת מהתוכניות, כתלות בכמות האיברים. שימו לב -
זמן הביצוע מושפע ממהירות המחשב עליו מבצעים את הבדיקות, כמות הזיכרון וכו':
| /מבנה הנתונים כמות האיברים/ |
רשימה | מערך | תור דו-כיווני |
|---|---|---|---|
| 10 | 0:00:02 | 0:00.02 | 0:00.02 |
| 1,000 | 0:00:02 | 0:00.02 | 0:00.02 |
| 10,000 | 0:00:09 | 0:00.09 | 0:00.03 |
| 100,000 | 0:19.70 | 0:21.93 | 0:00.17 |
| 200,000 | 2:25:50 | 2:28.38 | 0:00.33 |
כעת, בואו נסתכל על תוכניות אחרות, כדי להשוות את מהירות ביצוע גישה לפי אינדקס למבני הנתונים הללו. שלושת התוכניות הבאות מבצעות את הפעולה הזו - יצירת רשימה סדורה של מספרים, הכנסתם למבנה הנתונים, ולבסוף ביצוע שליפה אקראית של איברים מהרשימה - כשמספר פעולות השליפה הוא במספר האיברים הרשימה. כמו מקודם, התוכנית הראשונה משתמשת ברשימה, התוכנית השניה משתמשת במערך, והשלישית משתמשת בתור דו-כיווני.
תוכנית א' - עם רשימה (list).
#!/usr/bin/env python2.4
import sys
import random
if (not len(sys.argv) == 2):
print "Usage: ", sys.argv[0], "<number of elements>"
sys.exit(1)
elem_count = int(sys.argv[1])
print "elem_count - ", elem_count
# create a list with the given number of elements.
elem_id = 0
list = []
while elem_id < elem_count:
list.append(elem_id)
elem_id = elem_id + 1
# lookup 'elem_count' random elements in the list.
random.seed(1000)
elem_id = 0
while elem_id < elem_count:
list[random.randint(0, elem_count - 1)]
elem_id = elem_id + 1
print "done"
תוכנית ב' - עם מערך (array).
#!/usr/bin/env python2.4
import sys
import random
import array
if (not len(sys.argv) == 2):
print "Usage: ", sys.argv[0], "<number of elements>"
sys.exit(1)
elem_count = int(sys.argv[1])
print "elem_count - ", elem_count
# create an array with the given number of elements.
elem_id = 0
arr = array.array('i')
while elem_id < elem_count:
arr.append(elem_id)
elem_id = elem_id + 1
# lookup 'elem_count' random elements in the array.
random.seed(1000)
elem_id = 0
while elem_id < elem_count:
arr[random.randint(0, elem_count - 1)]
elem_id = elem_id + 1
print "done"
תוכנית ג' - עם תור דו-כיווני (deque) - נתמך מגירסא 2.4 של פייתון.
#!/usr/bin/env python2.4
import sys
import random
from collections import deque
if (not len(sys.argv) == 2):
print "Usage: ", sys.argv[0], "<number of elements>"
sys.exit(1)
elem_count = int(sys.argv[1])
print "elem_count - ", elem_count
# create a deque with the given number of elements.
elem_id = 0
dq = deque([])
while elem_id < elem_count:
dq.append(elem_id)
elem_id = elem_id + 1
# lookup 'elem_count' random elements in the deque.
random.seed(1000)
elem_id = 0
while elem_id < elem_count:
elem = dq[random.randint(0, elem_count - 1)]
elem_id = elem_id + 1
print "done"
הבה נשווה את זמן הביצוע של כל אחת מהתוכניות, כתלות בכמות האיברים. שימו לב -
זמן הביצוע מושפע ממהירות המחשב עליו מבצעים את הבדיקות, כמות הזיכרון וכו':
| /מבנה הנתונים כמות האיברים והשליפות/ |
רשימה | מערך | תור דו-כיווני |
|---|---|---|---|
| 10 | 0:00:02 | 0:00.02 | 0:00.02 |
| 1,000 | 0:00:03 | 0:00.03 | 0:00.03 |
| 10,000 | 0:00:09 | 0:00.09 | 0:00.09 |
| 100,000 | 0:00.75 | 0:00.76 | 0:01.17 |
| 200,000 | 0:01.49 | 0:01.50 | 0:03.87 |
| 400,000 | 0:03.00 | 0:02.99 | 0:35.70 |
| 800,000 | 0:05.94 | 0:05.99 | 4:59.41 |
שיעורון ב' - עצים
עצים הם צמחים גדולים בעלי מוט מרכזי הקרוי גזע, המתפצל לענפים ובסוף לעלים (ירוקים, בדרך כלל). עצים עשויים לחיות במשך מאות שנים, אם לא כורתים אותם קודם לכן. ארר.... מה, אנחנו לא בשיעור טבע? או, סליחה! הבה נתחיל מחדש...
מהו עץ? למה הוא טוב?
עץ הוא סוג של גרף המקיים את התנאים הבאים:
- הגרף קשיר (כלומר, יש מסלול מכל צומת בגרף לכל צומת אחרת).
- מכל צומת בעץ יש רק מסלול אחד לכל צומת אחרת.
- אם הגרף מכוון, אז יש לגרף צומת אחד הקרוי "שורש", ומסלול ממנו לכל אחד מהצמתים האחרים בגרף, אבל אין מסלול מאף צומת אחר בגרף לצומת השורש.
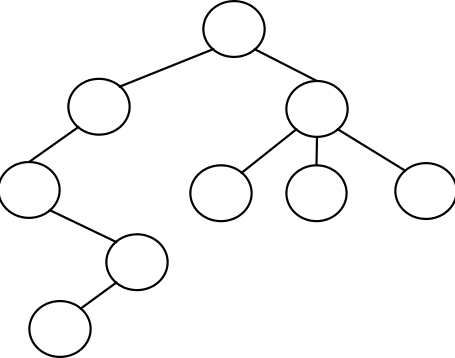
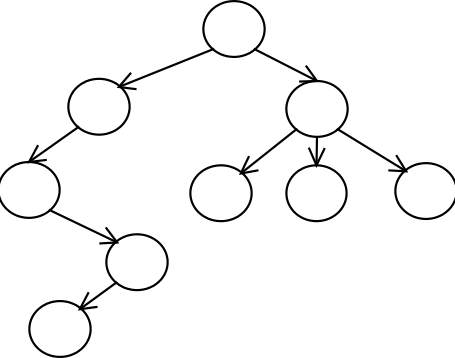
הנה דוגמא לעץ מכוון:
עצים ניתנים לחלוקה היררכית - לצומת השורש יש בנים - כל הצמתים שאליהם הוא מקושר ישירות, וצומת השורש הוא האבא שלהם. לכל צומת בן יכולים להיות גם כן צמתים בנים, וכן האה וכן הלאה...
עצים נוחים מאוד לשמירת מידע היררכי - למשל, תאור המבנה הניהולי של חברה, תיאור רשימת המשחקים בטורניר ספורט, תיאור חישוב המהלכים האפשריים במשחק דמקה... עצים מתת-משפחה הקרויה "עצים מאוזנים" יעילים מאוד בשמירת נתונים ממויינים (כפי שנראה כשנדון במיונים). העץ הוא מבנה נתונים שנשמע כמו אחד שכדאי להכיר. אז הבה נכיר אותו יותר טוב...
סוגי עצים - מאוזנים, בינאריים, כלליים...
עצים, כמו בטבע, מתחלקים לתת-משפחות, לפי תכונות שונות שלהם. אם בטבע מחלקים אותם לפי צבע העלים, מבנה הגזע וסוגי הזרעים, הפרופסורים שלנו (זוכרים אותם?) מחלקים אותם לתת-משפחות לפי המבנה הטופולוגי שלהם ("טופולוגי" זו מילה מסובכת שבאה לאמר שגם אם נזיז את הצמתים שמאלה וימינה ונעוות את הקשתות - מבנה העץ, מבחינת חיבורי הצמתים והקשתות לא ישתנה). כמו כן, ניתן לחלק את העצים לתת-משפחות לפי המידע השמור בצמתים ובקשתות.
ראשונים בסך צועדים להם העצים הבינאריים. בעץ בינארי, לכל צומת יש לכל היותר שני ילדים ישירים. ייתכן שלצומת יהיה רק בן אחד, וייתכן שלצומת לא יהיו כלל בנים. צומת ללא בנים, אגב, נקרא עלה. הצים בינאריים נוחים לטיפול בגלל המבנה הפשוט שלהם, כפי שנראה מאוחר יותר.
אחרי העצים הבינאריים מגיעים, רבותי וגבירותי, העצים המאוזנים. הבה נסתכל בתת
המשפחה של העצים הבינאריים המאוזנים - אלו עצים שבהם המסלול הארוך ביותר גדול, לכל
היותר, מהמסלול הקצר ביותר. העץ הבינארי ה"מאוזן" ביותר הוא עץ שבו כל המסלולים הם
בדיוק באותו האורך - והוא נקרא גם "עץ בינארי מלא". למשל, עץ בינארי מלא בעומק 3
נראה כך:
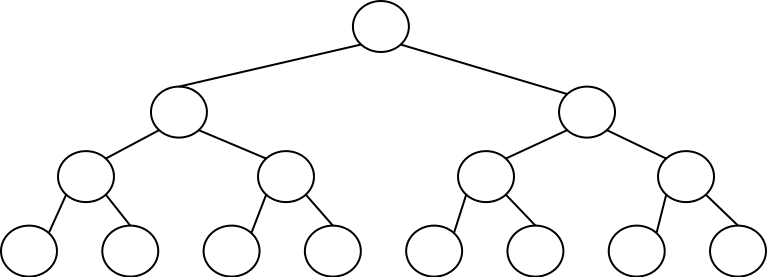
תכונה זו של עצים בינאריים מאוזנים הופכת אותם לאמצעי מצויין על-מנת לנהל באמצעותם
מתונים ממויינים - כפי שנראה כשנדבר בהמשך על מינויים.
אחת התכונות של צומת בעץ נקראת "דרגה". הדרגה של הצומת היא כמות הבנים שיש לצומת. לצומת בלי בנים יש דרגה 0. לצומת עם בן אחד יש דרגה 1, לצומת עם שני בנים יש דרגה 2, וכן הלאה. לעץ יש דרגה N אם יש בו לפחות צומת אחת עם דרגה N, ואף צומת עם דרגה גדולה יותר. כעת חישבו - לאיזה עץ יש דרגה 0? תשובות בסוף...
טיולים על עצים
אחד הדברים שאפשר לעשות עם עצים, הוא לטייל עליהם. כמו חיפושית שמטיילת על עץ תות, כך יכולים אנחנו לטייל על עצים. הפרופסורים פיתחו שיטות שונות לטיול על עצים, כשלכל אחת יש שימושים משלה. שלושת השיטות הבסיסיות הן טיול prefix, טיול postfix וטיול infix. כדי להבין מה משמעות המילים הלועזיות הללו, בואו נתמקד בעצים בינאריים, ובפעולת הדפסת הערכים הרשומים בצמתים (בהנחה שיש שם ערכים).
הדפסה בשיטת טיול prefix
בשיטת טיול זו, אנחנו מבצעים את האלגוריתם הבא:
- גשו לצומת השורש של העץ. הדפיסו את הערך שרשום בצומת זו.
- אם יש לשורש בן שמאלי, בצעו עבורו הדפסה בשיטת prefix.
- אם יש לשורש בן ימני, בצעו עבורו הדפסה בשיטת prefix.
למשל, עבור העץ הבא:
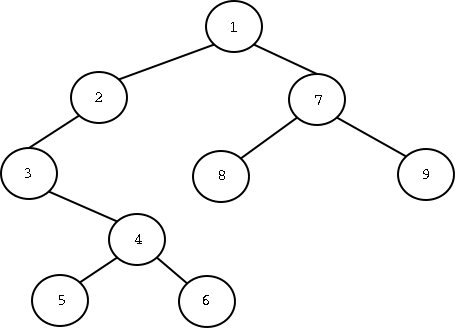
יודפסו המספרים הבאים (מימין לשמאל): 1, 2, 3, 4, 5, 6, 7, 8, 9
הדפסה בשיטת טיול postfix
בשיטת טיול זו, אנחנו מבצעים את האלגוריתם הבא:
- אם יש לשורש בן שמאלי, בצעו עבורו הדפסה בשיטת postfix.
- אם יש לשורש בן ימני, בצעו עבורו הדפסה בשיטת postfix.
- גשו לצומת השורש של העץ. הדפיסו את הערך שרשום בצומת זו.
עבור העץ הקודם, יודפסו המספרים הבאים (מימין לשמאל): 5, 6, 4, 3, 2, 8, 9, 7, 1
הדפסה בשיטת טיול infix
אחרונה חביבה, אך שימושית מכולן, היא שיטת infix. בשיטת טיול זו, אנחנו מבצעים את האלגוריתם הבא:
- אם יש לשורש בן שמאלי, בצעו עבורו הדפסה בשיטת infix.
- גשו לצומת השורש של העץ. הדפיסו את הערך שרשום בצומת זו.
- אם יש לשורש בן ימני, בצעו עבורו הדפסה בשיטת infix.
עבור העץ הקודם, יודפסו המספרים הבאים (מימין לשמאל): 3, 5, 4, 6, 2, 1, 8, 7, 9
תארו לכם עץ המתאר ביטוי מתמטי, למשל:
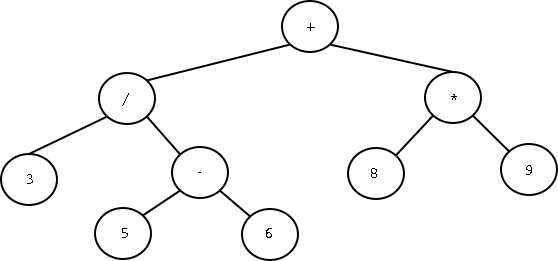
עבור עץ זה, טיול infix ידפיס את התוכן הבא (הפעם משמאל לימין):
את הסוגריים הוספנו כדי לשמור על סדר פעולות החשבון שהעץ מייצג.
בניית עצים בפייתון
הבה ונצמיח לנו עצי פייתון. יש דרכים שונות לגדל עצים - נבחן כמה מהן, ונשווה. בהדגמות אלו נתמקד בעצים בינאריים, על מנת לשמור על פשטות הקוד.
לפני שנבחן שיטות שונות למימוש עצים בפייתון, הבה נסתכל על כמה עקרונות מנחים:
- יש לאפשר לבנות עצים שלצמתים בהם אין אף בן (עלה), יש בן ימני בלבד, בן שמאלי בלבד או שני בנים.
- צריכה להיות אפשרות לשנות את תכונות צומת אחרי שנבנה העץ.
- צריכה להיות אפשרות לשנות את מבנה העץ - להוסיף צמתים, למחוק צמתים...
עצים מרשימות
שיטה אחת היא להשתמש ברשימות. רשימות בפייתון ניתנות לכינון. "מה זה כינון" אתם שואלים את עצמכם? פרושו של דבר, שאיבר ברשימה יכול להיות רשימה נוספת. הנה דוגמא:
scary_list = [[1, 2, 3], 4, [5, 6], [7, [8, 9]]]
- צומת עלה ייוצג על-ידי רשימה בעלת איבר אחד בלבד. האיבר הזה יהיה המספר שרשום בצומת.
- צומת שאינו עלה ייוצג על-ידי רשימה המכילה 3 איברים. האיבר הראשון יהיה המספר שרשום בצומת. האיבר השני יהיה הבן השמאלי של הצומת. האיבר השלישי יהיה הבן הימני של הצומת.
- אם לצומת יש בן שמאלי ולא ימני, הוא ייוצג על-ידי רשימה באורך 3 איברים - הראשון מכיל את המספר שרשום בצומת, השני מכיל את הבן השמאלי והשלישי מכיל רשימה ריקה.
- אם לצומת יש בן ימני ולא שמאלי, הוא ייוצג על-ידי רשימה באורך 3 איברים - הראשון מכיל את המספר שרשום בצומת, השני מכיל רשימה ריקה, והשלישי מכיל את הבן הימני.
-
--- | 4 | --- - [ 4 ]
-
--- | 7 | --- \ / \ / --- --- | 8 | | 3 | --- --- - [ 7 [ 3 ] [ 8 ] ]
-
--- | 7 | --- \ / \ / --- --- | 8 | | 3 | --- --- \ \ / \ \ / --- --- --- | 2 | | 9 | | 4 | --- --- --- - [ 7 [3 [ 4 ] [ 9 ]] [ 8 [] [ 2 ]] ]
הנה פונקציה שבונה עץ מלא בעל עומק נתון, ובכל צומת רושמת את מיספרו הסידורי לפי סיור infix. שימו לב לרעיון המהפכני - הפונקציה קוראת לעצמה - פעולה זו נקראת בשם רקורסיה (recursion).
def build_full_bin_tree(depth, num):
if depth == 0:
return [num]
left = build_full_bin_tree(depth - 1, num - ((2**depth)/2))
right = build_full_bin_tree(depth - 1, num + ((2**depth)/2))
return [num, left, right]
שימו לב לתרגיל המוזר עם המספר הרשום בצומת (הפרמטר num של הפונקציה) - נסו לחשוב מדוע אנחנו משחקים עם המספר באופן כה מוזר בעת הקריאה הרקורסיבית לפונקציה. רמז - אם קוראים לפונקציה עם depth=3, יש להעביר לה num=8 (2 בחזקת 3).
וכעת פונקציה המדפיסה את תוכנו של עץ כזה "על הצד":
def print_tree_infix(tree, indent_level):
if len(tree) == 1: # a leaf - it must contain a single number
print " " * indent_level * 2, tree[0]
else: # a non-leaf node - this must be a list with 3 elements.
if len(tree[1]) < 0: # there is a left child
print_tree_infix(tree[1], indent_level + 1)
print " " * indent_level * 2, tree[0]
if len(tree[2]) < 0: # there is a right child
print_tree_infix(tree[2], indent_level + 1)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
עצים בעזרת מילונים
שיטה נוספת לבניית עצים היא להשתמש במילונים. לשם כך נייצג כל צומת באמצעות מילון, באופן הבא:
- כל צומת ייוצג על-ידי מילון בעל מפתח בשם 'v', שהערך שלו הוא המספר שרשום בצומת.
- אם לצומת יש בן שמאלי, יהיה במילון שלו מפתח 'l', שהערך שלו הוא הבן השמאלי של הצומת.
- אם לצומת יש בן ימני, יהיה במילון שלו מפתח 'r', שהערך שלו הוא הבן הימני של הצומת.
הנה פונקציה רקורסיבית (כלומר, פונקציה הקוראת לעצמה) שבונה עץ מלא בעל עומק נתון, ובכל צומת רושמת את מיספרו הסידורי לפי סיור infix.
def build_full_bin_tree(depth, num):
if depth == 0:
return {'val': num}
left = build_full_bin_tree(depth - 1, num - ((2**depth)/2))
right = build_full_bin_tree(depth - 1, num + ((2**depth)/2))
return {'val': num, 'left': left, 'right': right}
וכעת פונקציה המדפיסה את תוכנו של עץ כזה "על הצד":
def print_tree_infix(tree, indent_level):
if tree.has_key('left'):
print_tree_infix(tree['left'], indent_level + 1)
print " " * indent_level * 2, tree['val']
if tree.has_key('right'):
print_tree_infix(tree['right'], indent_level + 1)
כפי שניתן לראות, הפונקציות הללו פשוטות יותר מאשר הפונקציות שטיפלו בעצים המורכבים מרשימות מכוננות (זוכרים מה זה אומר?). כעת בוודאי תשאלו "למה לא להשתמש במילונים וזהו?". התשובה תהיה, מן הסתם, שמילונים דורשים יותר זיכרון מאשר רשימות. כלומר, כשעובדים עם מספר קטן של עצים קטנים, פשוט יותר להשתמש במילונים. כשעובדים עם מספר גדול מאוד של עצים, או עם עצים גדולים מאוד, עדיף להשתמש ברשימות.
משחקי עצים
על-מנת לתרגל מעט את השימוש בעצים, נסו לכתוב תוכנית המדמה טורניר טניס. למי שלא מכיר - בטורניר, משבצים את השחקנים לשחק בזוגות. המפסידים יוצאים מהטורניר, ואילו המנצחים עולים לשלב הבא ומשחקים שוב בזוגות (בשלב הזה יש חצי ממספר הזוגות). הטורניר נמשך עד שנותר זוג אחד המשחק במשחק הגמר, והמנצח במשחק זה זוכה בטורניר.
לתוכנית יש רשימת שמות של שחקנים הרשומה במשתנה גלובלי. למשל:
שימו לב שכדי שהטורניר יהיה מושלם, יש צורך שמספר השחקנים יהיה חזקה של 2 (כלומר מספר השחקנים יכול להיות 2, 4, 8, 16 וכן הלאה). - הדמיה של טורניר טניס (ישנה רשימת שחקנים, משבצים אותם למשחקים בטורניר על-ידי שימוש במבנה של עץ בינארי מאוזן, מדמים את המשחקים, מציגים את תוצאותיהם לפי הטורניר, ובסוף מכריזים על המנצח).
התוכנית צריכה "להגריל" שחקנים למשחקים, על-ידי בניית עץ מלא שבכל אחד מהעלים יש שם של אחד השחקנים. המשחקים מנוהלים העץ על ידי טיפוס כלפי מעלה - לכל שני עלים בעלי צומת-אב משותף, מנהלים "משחק" (הגרלה אקראית) שקובע מי משני השחקנים ניצח. את שמו של המנצח מעתיקים לצומת האב. לאחר שביצענו פעולה זו עבור כל העלים, עוברים לבצע את אותה הפעולה עבור רשימת האבות (השיכבה הבאה של העץ). ממשיכים עד שמגיעים לשורש - ובשורש יהיה רשום שמו של המנצח. שימו לב - צורת הטיול המתאימה לניהול הטורניר היא שיטת postfix.
על התוכנית להדפיס את רשימת המשחקים בכל אחד משלבי הטורניר, ועבור כל משחק לרשום את שמו של המנצח. יש לדאוג שההדפסה תהיה נוחה לקריאה.
שיעורון ג' - עצים למשחקי מחשבה - עצי מיני-מקס
אחד התחומים המעניינים בכתיבת תוכנה הוא בינה מלאכותית - היכולת לכתוב תוכנה שתגרום לנו להרגיש שהמחשב חושב. עולם התוכניתנים מתחלק לשתי קבוצות - זו שמוצאת את הרעיון הזה מרתק, וזו שכבר התייאשה והחליטה שזה בלתי אפשרי. אם אתם שייכים לקבוצה הראשונה, המשיכו וקיראו. אם לא - דלגו על הפרק הזה והפרק הבא...
רוב הטכניקות הקיימות היום בתחום הבינה המלאכותית מתמצות ברעיון הבא - כל בעיה שניתן להגדירה על פי חוקים ברורים, ניתנת לפיתרון על-ידי בחינת כל האפשרויות המקיימות את החוקים (למשל במשחק דמקה - אם המחשב יבדוק את כל המהלכים האפשריים, הוא ימצא את המהלכים הטובים ביותר שיש). שתי בעיות יש בגישה זו:
- לפעמים מספר האפשרויות שיש לבחון הוא עצום - צריך להחליט אילו אפשרויות לבדוק קודם, ועל אילו לדלג, אחרת יעברו שנים עד שהמחשב יספיק לבחון את כל האפשרויות.
- איך מחליטים אם אפשרות מסויימת טובה יותר מהשניה? צריך "ללמד" את המחשב לדעת מה יותר מוצלח, ומה פחות מוצלח.
להסבר מפורט יותר על משחקי סכום-אפס, הציצו בערך של משחקי סכום-אפס בוויקיפדיה.
איך מחשב יכול לשחק שחמט, דמקה או רברסי?
כדי שמחשב יוכל לשחק במשחק כלשהו, הוא צריך להכיר את חוקי המשחק (בעיקר - כיצד מותר להזיז את הכלים על לוח המשחק), וכן כיצד מעריכים כמה עמדה מסויימת טובה עבור אחד השחקנים. כעת, כל מה שתוכנת המשחק צריכה לעשות ,בהינתן מצב נתון במשחק, הוא לחשב את כל המהלכים האפשריים ממצב זה, ולראות איזה מהם מוביל למצב משחק הטוב ביותר עבור המחשב - ואז לבצע את המהלך המתאים.
כמובן שבצורת עבודה זו יש חיסרון - לפעמים כדאי לבצע מהלך שאינו הכי טוב כרגע, אולם יאפשר לתוכנה לבצע בתור הבא מהלך מבריק ביוביל אותו למצב טוב בהרבה. לפעולה זו (ביצוע מהלך חלש לכאורה כדי לבצע אחריו מהלך מבריק) נקרא בשם "תחבולה". לפעמים תחבולה אינה ניתנת לביצוע בשני מהלכים - ייתכן שיש צורך בשלושה או ארבעה מהלכים לשם ביצוע התחבולה. ככל שהמחשב ייחשב יותר מהלכים קדימה, הוא ייקח בחשבון יותר תחבולות אפשריות, ולכן יש סיכוי יותר טוב שינצח.
כמובן, הכל היה פשוט אם המחשב היה משחק לבד. במציאות, המחשב משחק נגד יריב כלשהו (אדם, או אולי תוכנת מחשב אחרת?). השחקן היריב כמובן שלא יתפתה לבצע מהלך שיעזור לתוכנת המחשב שלנו - להיפך, הוא ינסה לבצע את המהלך הטוב ביותר עבורו, שהוא המהלך הרע ביותר עבור תוכנת המחשב. לכן, כשהמחשב מנסה לתכנן איזה מהלך לבצע, עליו לקחת בחשבון שהשחקן היריב פועל בשיטות דומות, ולכן בכל פעם שתורו לשחק, יבחר את המהלך הגרוע ביותר עבור המחשב. תחבולה תפעל רק אם היא לא תלויה המהלך שיבצע השחקן היריב, או אם כל מהלך אחר שיבצע יוביל אותו למצב גרוע עוד יותר.
לעשות: לתת דוגמא קונקרטית ממשחק דמקה, על הקרבת כלי כדי להרוויח מלכה.
מהם עצי מיני-מקס?
עצי מינימקס הם תת-משפחה של עצים המאפשרים לבצע את חישוב המהלך הבא לפי השיטה שהצגנו. כל צומת בעץ מינימקס מתאר מצב של המשחק (למשל סידור כלים כלשהו על לוח דמקה). צומת השורש של עץ המינימקס מתארת את מצב הלוח הנוכחי. לצומת זו יש צמתים-בנים שמספרם הוא כמספר המהלכים החוקיים שהמחשב יכול לבצע, על פי חוקי המשחק. לכל צומת-בן כזו יש צמתים-בנים כמספר המהלכים החוקיים שיכול לבצע השחקן היריב מהמצב המתואר בצומת זו. וכך הלאה, עד לדרגת עומק שנקבעת לפי כמות הזיכרון ומגבלות כוח-החישוב העומד לרשות המחשב, ולפי משך הזמן שהשחקן היריב יסכים לחכות לביצוע מהלך של המחשב, לפני שהוא יתרגז ו-"יהפוך את הלוח" (כלומר - יסגור את תוכנת המשחק).
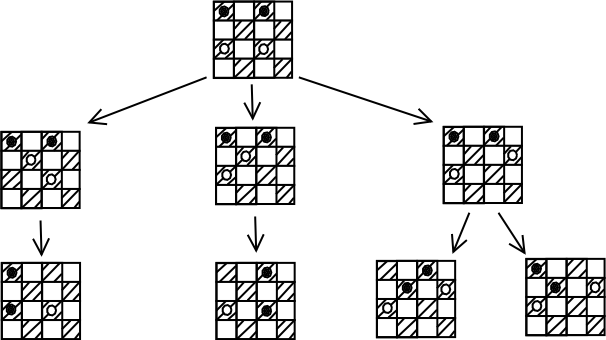
לשם המחשה, בואו ניקח מצב במשחק דמקה על לוח מוקטן (ארבע שורות על ארבע עמודות),
ונבנה את עץ המינימקס עבור 2 מהלכים (כלומר, מהלך אחד של המחשב, ותגובה אחת של
היריב). בדוגמא שלנו המחשב משחק בכלים הלבנים. שימו לב - בדמקה שלנו, החוקים
אומרים שמותר להזיז כלים רק קדימה, ואם יש לנו אפשרות "לאכול" כלי של היריב -
אנחנו חייבים לאכול - אסור לנו לבצע במקום זה מהלך אחר. אם יש לנו כמה אפשרויות
"לאכול" כלי של היריב - חייבים לבצע אחת מהן.
פונקציות הערכת מצבים.
לאחר שתוכנת המחשב בנתה את העץ, היא צריכה להעריך את "שווי" כל אחד מהלוחות שבעץ. לשם כך יש צורך בפונקציית הערכה. פונקצייה זו, בהינתן מצב לוח, מחשבת מספר המהווה את "שווי מצב הלוח עבור המחשב". ככל שהמספר הזה גבוה יותר - מצב הלוח טוב יותר למחשב (ורע יותר לשחקן היריב).
הבה ונבחר פונקצית הערכת מצב, ונחשב את ערכה עבור כל מצבי הלוחות שבעלים של העץ שבנינו. הבה נבחר פונקציה פשוטה (אבל לא פשוטה מדי), האומרת כך:
- נוסיף 5 נקודות עבור כל כלי רגיל שלנו, ו-15 נקודות עבור כל מלכה שלנו.
- נחסיר 5 נקודות עבור כל כלי רגיל של השחקן היריב, ו-15 נקודות עבור כל מלכה של השחקן היריב.
- נוסיף נקודה עבור כל "דרגת חופש" לכל כלי שלנו. דרגת חופש פרושה משבצת שאליה יכול לנוע הכלי שלנו. אנחנו מניחים שככל שלכלי שלנו יש יותר אפשרויות לנוע, מצבנו טוב יותר.
- נוריד נקודה עבור כל "דרגת חופש" לכל כלי של המחשב.
הבה ונראה את העץ עם תוצאות חישוב הפונקציה לכל אחד מהעלים:
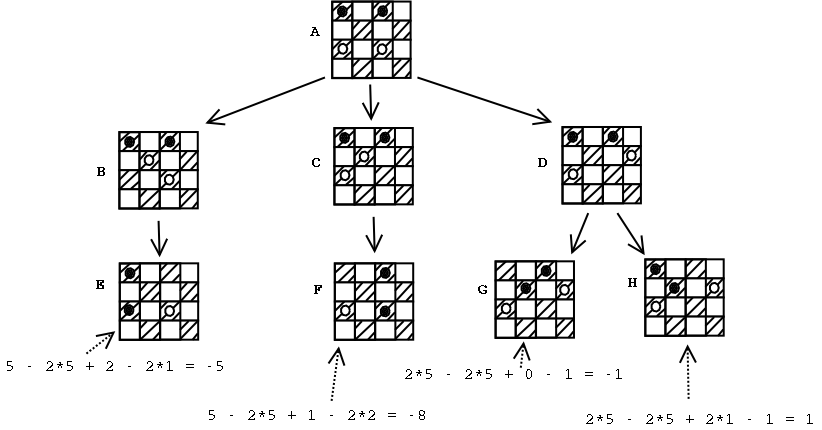
כפי שניתן לראות, הלוח הימני התחתון הוא הטוב ביותר עבורנו, ולכן אליו אנחנו
צריכים לשאוף להגיע.
מבנה המשחק על-ידי שימוש בעץ מיני-מקס.
אחרי שהישקנו את העץ והוא גדל, וחישבנו את ערכם של העלים, מה שחסר לנו הוא הידע איך להגיע ללוח הכי טוב. לכאורה, ניקח את הלוח הכי טוב, נטפס ממנו במעלה העץ, ואז נמצא את סידרת המהלכים שיובילו אותנו לשם. אלא מה? אנחנו מניחים שהיריב משתף איתנו פעולה. הנחה שפויה אם אנחנו משחקים את שני הצדדים. בפועל, היריב ינסה לבצע את ההפך - הוא ישחק את המהלכים שיובילו את המשחק למצב הלוח הרע ביותר עבורנו. כלומר, אם בכל תור שלנו נבחר את המהלך שיביא אותנו ללוח עם הניקוד הגבוה ביותר, הרי שהיריב, בכל תור שלו, יבחר את המהלך שיוביל ללוח עם הניקוד הנמוך ביותר.
אז כיצד יודעים איך לשחק? התשובה היא - מתחילים מהסוף. נניח שהגענו למצב הלוח של צומת D. מי שיבצע את המהלך הבא מצומת זו הוא היריב, והוא יכול לבחור בין המהלך המוביל לעלה G, למהלך המוביל לעלה H. מן הסתם, היריב יעדיף להמשיך למצב הלוח בעל הניקוד הנמוך יותר (עלה G, עם ניקוד -1). לכן, אפשר לסמן את צומת D בניקוד -1. מצומת C אפשר להגיע רק אל עלה F, ולכן ניתן לסמן את צומת C בציון -8. באופן דומה, נסמן את צומת B בציון -5.
כעת נעלה שכבה אחת למעלה - לצומת A. מי שמבצע את המהלך מצומת A הוא המחשב. המחשב שואף להגיע לצל לוח בעל הניקוד הגבוה ביותר, ולכן הוא יבחר לעבור לצומת-הבן בעל הניקוד הגבוה ביותר - כלומר לצומת D. לפיכך, הניקוד של צומת A יהיה -1.
לפיכך, המהלך שעל המחשב לבצע הוא במהלך המוביל מצומת A לצומת D. שימו לב שהניקוד של הלוח שלילי - כלומר המסע מוביל את המחשב למצב לא טוב. עדיין, המצב פחות רע מאשר בבחירת אחד המהלכים האפשריים האחרים.
אם נתרגם את תהליך ה-minimax הזה לאלגוריתם מסודר, הוא יראה דומה לטיול postfix, בגרסא לעץ בעל דרגה לא חסומה (כלומר, לצומת עשויים להיות מספר רב של בנים):
- בצע חישוב minimax עבור כל אחד מהבנים של הצומת הנתונה.
- אם הצומת הנתונה בעומק זוגי (כלומר מי שמבצע מהלך ממנה הוא המחשב), מצא את הציון הגבוה ביותר של כל הצמתים-הבנים של הצומת, ורשום אותו בצומת.
- אחרת (אנחנו בעומק בלתי-זוגי) - מצא את הציון הנמוך ביותר של כל הצמתים-הבנים של הצומת, ורשום אותו בצומת.
מימוש עץ מיני-מקס בפייתון.
לעשות...